최근 David Silver 교수의 Reinforcement Learning Course 를 보면서 강화학습에 대해 공부하다 연장선상으로 뒤늦게 AlphaGo 논문을 읽었습니다. 바둑에 대해 전혀 모르더라도 AlphaGo 가 어떻게 동작하는지는 이해할 수 있었습니다. 벌써 2-3년이 지난 논문이지만 간단하게 정리해봤습니다.

AlphaGo Lee

AlphaGo Lee 는 2016년 3/9 부터 3/15 까지 프로바둑 기사 이세돌과 바둑 게임을 한 딥러닝 모델입니다. 이세돌과 경기를 하기 전에는 유럽 바둑대회를 우승했던 Fan Hui 와 붙어 이겼습니다. AlphaGo 는 크게 AlphaGo Lee / AlphaGo Zero 버전으로 나뉘는데 여기서는 AlphaGo Lee 만 정리하려 합니다.

바둑은 두 플레이어가 각각 흑백 돌을 두면서 많은 진영을 가진 자가 이기는 게임입니다. 돌을 두기까지 제한된 시간을 쓸 수 있는데 AlphaGo 는 이 시간 동안 트리를 이용하여 경우의 수를 탐색한 후 가장 좋은 수를 둡니다. 이미 컴퓨터로 정복된 체스는 경우의 수가 $10^{120}$ 입니다. 하지만 바둑의 경우의 수는 $10^{170}$ 으로 모든 경우의 수를 계산하려면 컴퓨터로 수십억 년이 걸린다고 합니다. AlphaGo 는 이 많은 경우의 수를 어떻게 처리했을까요?

가능성이 있는 수들만 탐색해본다.

이기기 위해 굳이 엉뚱한 곳에 수를 두고 경우의 수를 탐색할 필요는 없습니다. 승산이 있어 보이는 곳에 수를 두고 그 이후 경우의 수를 탐색해보면 됩니다.

승산이 없는 게임은 굳이 더 탐색하지 않는다.

흔히 우리는 게임을 볼 때 어떤 상황에서 누가 이겼는지 졌는지를 판단하곤 합니다. 게임의 진행 정도가 지나면 지날수록 초보들도 누가 이겼는지 졌는지를 판단할 수 있습니다. 이처럼 이미 승패가 어느 정도 기운 상태에서는 굳이 그 이후의 수까지 탐색할 필요가 없습니다.

그러면 승산이 있을 만한 곳이 어디인지, 바둑판만 보고 내가 승산이 있는지 없는지는 어떻게 파악할까요?

필요한 Networks

이전에 언급했던 것과 같이 터무니없는 수를 두지 않기 위해, 바둑판을 보고 승산이 있는지 없는지를 알기 위해서는 몇 개의 준비물이 필요합니다.

1. SL policy network
2. Rollout policy network
3. RL policy network
4. Value network

SL Policy Network

Supervised Learning Policy Network 는 바둑판의 상태를 입력으로 다음 수가 어디에 놓일지 예측하는 Network 입니다. 다음 수를 어느 곳에 둘지 나타내는 확률 분포가 출력으로 나옵니다.

출처: Mastering the game of Go with deep neural networks and tree search

전문가들의 기보를 기반으로 트레이닝하여 다음 수를 예측하는 데 대략 57% 의 정확도를 보였다고 합니다.

Rollout Policy Network

위 SL Policy Network 와 같이 전문가의 기보를 학습시킵니다. 출력도 다음 수에 관한 확률 분포로 위의 Policy Network 와 거의 비슷합니다. 하지만 입력에 대해 CNN을 사용하지 않고 사람이 생각하는 특징들을 입력으로 받으며 상대적으로 SL Policy Network 보다 가볍게 만든 Network 입니다. 정확도는 24% 정도로 SL Policy Network 보다 많이 낮습니다. 하지만 처리 시간은 $2{\mu}s$ 로 $3ms$ 걸리는 SL Policy Network 보다 1,000배가 넘게 빠릅니다.

RL Policy Network

Reinforcement Learning Policy Network 로 Network 끼리 플레이를 하면서 Game 을 이기는 방향으로 성장합니다. Network 구조는 SL Policy Network 와 같습니다. 초기 사이사이 Weight 도 SL Policy Network 와 같은 값으로 초기화합니다. 경쟁 상대는 학습시켜오던 과정 중에 있던 Network 들을 모아 임의로 추출합니다. 예를 들면 SL Policy Network, 500번 학습한 RL Policy Network, 1000번 학습한 RL Policy Network ... 와 같이 Opponent Pool 에 저장한 후 이 Pool 에서 임의로 선택한 Network 와 시합을 하며 성장합니다. Overfitting 을 막기 위해 많이 학습한 RL Policy Network 끼리 학습시키지 않고 다양한 적들과 상대합니다. 나중에 결과물의 RL Policy Network 는 SL Policy Network 를 상대로 80% 승률을 보였다고 합니다. 정교한 MCTS 를 이용한 프로그램 Pachi 를 상대로는 85% 승률을 보였다고 합니다. SL Policy Network 는 Pachi 를 상대로 11% 승률을 보였다고 합니다.

Value Network

Value Network 는 바둑판의 상태를 보고 승률을 예측합니다. 위에서 설명한 Policy Network 들은 바둑판의 상태를 보고 다음 수에 대한 확률 분포를 내뱉습니다. 하지만 Value Network 는 같은 구조로 구성되지만, 승률만 내뱉습니다.

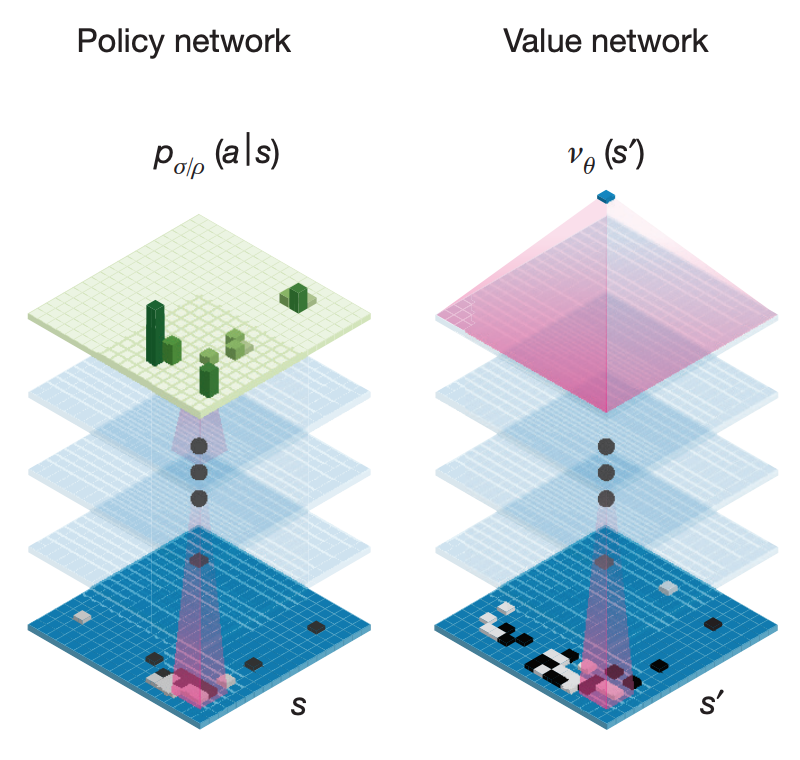
출처: Mastering the game of Go with deep neural networks and tree search

KGS 데이터로 학습시킨 Value Network 는 일반적으로 승률을 계산하기보다는 그전 결과들을 기억하여 트레이닝 데이터에서는 MSE 가 0.19이었지만 테스트 데이터에서는 0.37이 나왔습니다. 이러한 Overfitting 문제를 피하고자 RL Policy Network 끼리 경기한 3,000만 플레이 데이터를 모았다고 합니다.

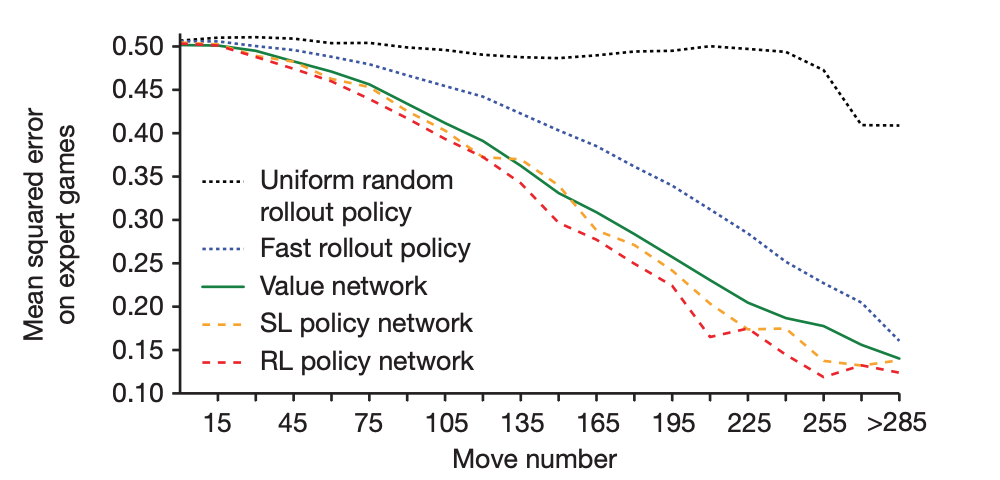
출처: Mastering the game of Go with deep neural networks and tree search

위에 표에서 X 축 오른쪽으로 갈수록 경기가 많이 진행됐음을 의미한다. 경기가 진행되면 될수록 초보자도 승패를 알 수 있으니 대체적으로 error 가 낮아집니다. 하지만 여기서 Policy Network 로 예측한 승률과 Value Network 의 승률 계산이 크게 차이 나지 않음을 볼 수 있습니다. Policy Network 가 수를 두면서 결괏값을 예측하는 것보다 바둑판의 상태를 보고 승률을 예측하는 Value Network 가 매우 빠르므로 Value Network 를 사용합니다.

MCTS: Monte Carlo Tree Search

Monte Carlo 는 계산하려는 값을 구하기 힘들 때 수많은 시도를 통해 근사적으로 계산하는 방법을 말한다. 아래 그림은 수많은 점을 찍어 원주율을 계산하는 과정입니다.

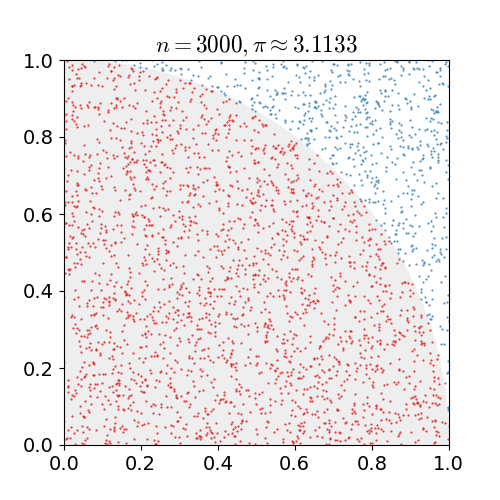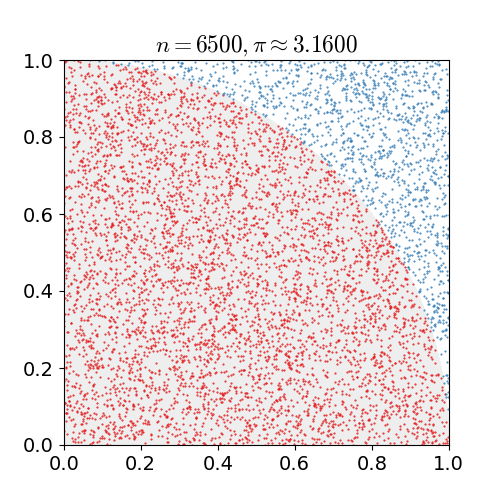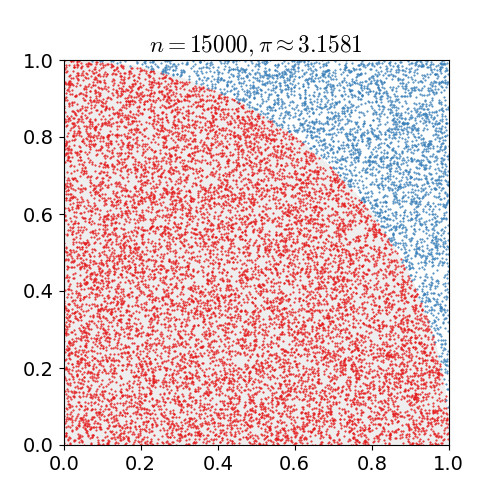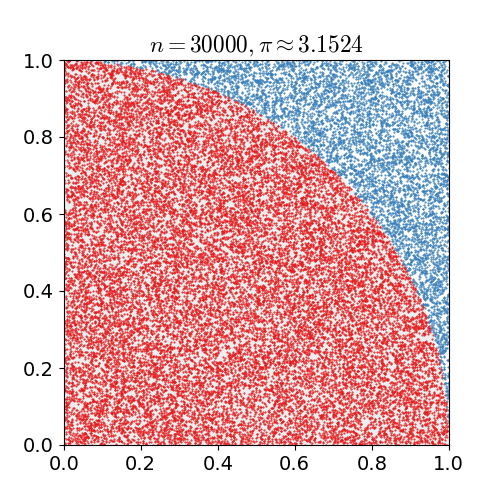
출처: 위키피디아 - 몬테카를로 방법

MCTS 는 가상으로 수많은 수를 두면서 트리를 구성하는 방식이다. 많은 게임을 하면 할수록 트리는 더 다양한 상황을 탐색하고 더 좋은 수를 알아낼 수 있습니다. MCTS 는 크게 4 step(Selection, Expansion, Evaluation, Backup) 으로 나눌 수 있습니다.

Selection, Expansion

MCTS 의 첫 과정 Selection, Expansion 은 SL Policy 를 이용하여 트리를 만들어나갑니다. 트리에는 상태 s 에서 행동 a 를 취했을 때 얼마만큼의 가치가 있는지를 나타내는 $Q(s, a)$, 방문 횟수 N(s, a) 그리고 사전확률 P(s, a) 등을 저장합니다.

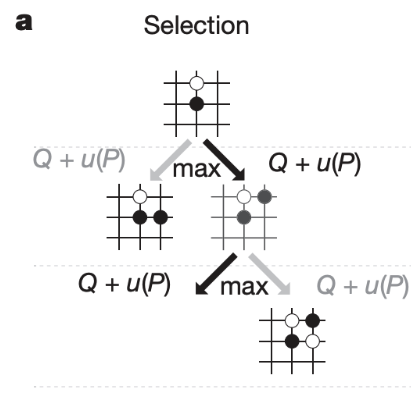
출처: Mastering the game of Go with deep neural networks and tree search

먼저 위 그림과 같이 루트에서 $Q+u(p)$ 큰 값의 상태를 따라 내려갑니다.

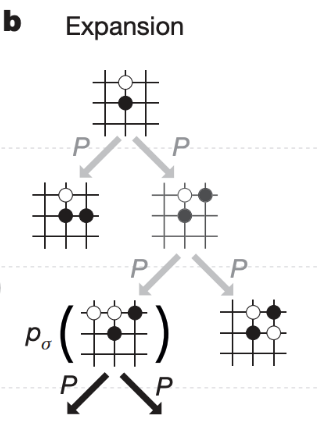
출처: Mastering the game of Go with deep neural networks and tree search

값이 높은 방향으로 선택하면서 내려가다가 이미 방문했던 상태 이외에 큰 $Q+u(p)$ 를 만나면 그림처럼 가지를 뻗어 나갑니다. $u(p)$ 는 $P(s, a) / N(s, a)$ 값에 비례합니다. 초기에는 exploration 관점에서 낮은 방문 횟수의 상태를 선호하지만, 점근적으로 $Q$가 큰 값을 선택합니다. 방문을 많이 하면 할수록 시뮬레이션을 많이 하고 $Q$ 값은 더 정교해집니다. 여기서 RL Policy Network 를 쓰지 않는 이유는 SL Policy Network 가 성능이 더 좋았다고 합니다.

Humans select a diverse beam of promising moves, whereas RL potimizes for the single best move

출처: Mastering the game of Go with deep neural networks and tree search

Evaluation

Selection, Expansion 으로 바둑돌을 놓은 후 얼마나 좋은 수인지 가치를 매깁니다.

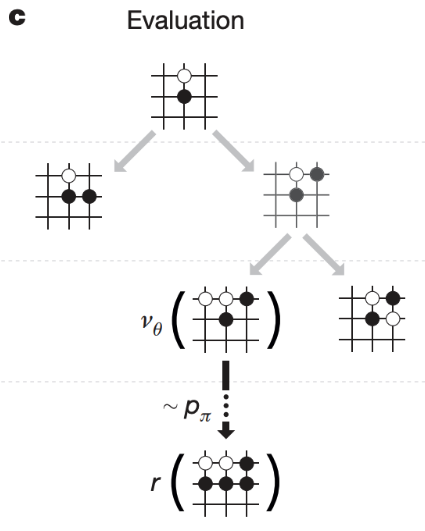
출처: Mastering the game of Go with deep neural networks and tree search

여기서 판단하는 방식이 2가지가 있는데, 첫 번째로는 Value Network 를 써서 바둑판의 상태를 보고 승률을 예측해봅니다. 두 번째로 위에서 언급했던 SL Policy Network 보다 가볍고 빠른 Rollout Policy Network 을 이용해서 가상으로 끝까지 게임을 플레이 합니다. 예를 들면 끝까지 게임을 두어서 내가 흑돌로 플레이 한 상태로 흑돌이 이겼으면 +1 졌으면 -1 보상을 받습니다. Value Network 의 값과 Rollout Policy Network 로 플레이한 게임의 결과를 합하여 그 수가 얼마나 좋은지 판단합니다.

Backup

이렇게 Selection, Expansion, Evaluation 을 해서 얻은 값을 지나온 경로의 상태들에 반영됩니다. 반영된 $Q$ 값을 보고 다음 Selection, Expansion, Evaluation 을 반복합니다.

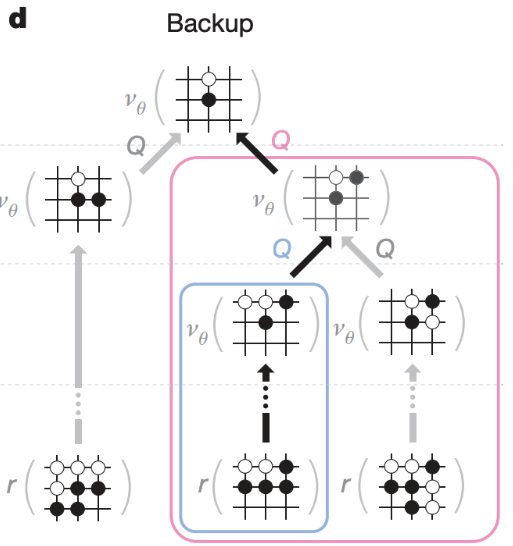
출처: Mastering the game of Go with deep neural networks and tree search

Conclusion

바둑에서는 셀 수 없이 많은 경우의 수가 존재하지만 AlphaGo 는 탐색할 경우의 수를 줄이면서 프로 바둑 기사에게 승리를 거둡니다. 수 읽기 시간에 많은 시뮬레이션을 통해 가능한 경우의 수들을 트리로 구성합니다. 트리를 구성하는 과정에서 전문가들의 기보를 학습한 Policy Network 로 가능성이 있는 수들만 탐색하고, Value Network 와 Rollout Policy Network 을 이용하여 승률을 예측합니다. 많은 수를 경험하면 트리의 정확도는 올라가지만 바둑에서는 시간이 제한적이기 때문에 탐색 수를 적절하게 조절해야 합니다. Atari 게임에서 강화학습을 이용한 사례들과는 다르게 사람의 기보를 기반으로 만든 Network 를 사용한다는 한계가 있습니다.